Answer:
tension in the string at the top position of the ball will be given as
T = 44.4 N
Step-by-step explanation:
At the top position of the trajectory we have force equation given as
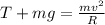
here we have
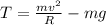
so we have
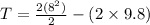
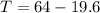
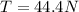
So tension in the string at the top position of the ball will be given as
T = 44.4 N