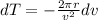Answer:
Part a)
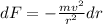
Part b)
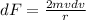
Part c)
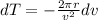
Step-by-step explanation:
Part a)
As we know that force on the passenger while moving in circle is given as
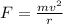
now variation in force is given as
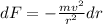
here speed is constant
Part b)
Now if the variation in force is required such that r is constant then we will have
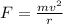
so we have
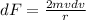
Part c)
As we know that time period of the circular motion is given as

so here if radius is constant then variation in time period is given as