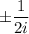Answer: Horizontal asymptote is
 and vertical asymptotes are
and vertical asymptotes are
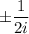
Explanation:
Since we have given that
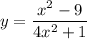
We need to find the horizontal and vertical asymptotes.
Since vertical asymptotes will occur where the denominator becomes zero.
So, here denominator is
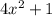
Now,
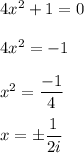
And the horizontal asympototes will occur when the coefficient of higher degree of numerator is divided by coefficient of higher degree of denominator.
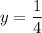
Hence, horizontal asymptote is
 and vertical asymptotes are
and vertical asymptotes are