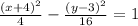Answer:
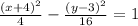
Explanation:
The hyperbola centered at (h,k) has the following expression:

Where
 and
and
 are the length of the horizontal and vertical semi-axes, respectively.
are the length of the horizontal and vertical semi-axes, respectively.
Since the center and one vertex share the same vertical component (
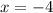 ), it is easy to conclude that hyperbola has a vertical configuration (
), it is easy to conclude that hyperbola has a vertical configuration (
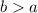 ). The distance between the center and the known vertex is equal to the length of the vertical semi-axis. Therefore:
). The distance between the center and the known vertex is equal to the length of the vertical semi-axis. Therefore:
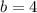
The slope of the hyperbola is given by the following relationship:
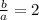
The length of the horizontal semi-axis is:
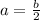
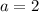
The standard form of the equation of the hyperbola is: