Question

given : AD is ⊥to AB and DC, BC is ⊥ to AB and DC, angle EDC ≅ angle ECD, AD ≅ BC. prove: triangle ADE ≅ triangle BCE

Answer 1

Hence proved triangle ADE ≅ triangle BCE by Side Angle Side congruent property.

Explanation:

Given:

AD ⊥ AB
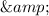`\&` CD

BC ⊥ AB
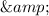`\&` CD

AD = BC

∴ ∠ A = ∠ B = ∠ C = ∠ D =90°

∠ EDC = ∠ ECD

Solution

∠ C = ∠ BCE + ∠ ECD⇒ equation 1

∠ D = ∠ ADE + ∠ EDC⇒ equation 2

∠ C = ∠ D (given)

Substituting equation 1 and 2 in above equation we get

∠ BCE + ∠ ECD = ∠ ADE + ∠ EDC

But ∠ EDC = ∠ ECD (given)

∴ ∠ ADE = ∠ BCE

ED = EC (∵ base angles are same triangle is isosceles triangle)

Now, In Δ ADE and Δ BCE

AD =BC

∠ ADE = ∠ BDE

ED = EC

∴ By Side Angle Side congruent property

Δ ADE ≅ Δ BCE