Answer:
$2368.68
Explanation:
Use the equation for total amount involving compound interest:
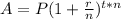
A is the total amount.
P is the principle, the starting investment.
r is the compound interest rate annually.
n is number of compounding periods in a year.
t is the number of years.
Substitute the values known into the equation.
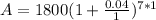
Simplify.

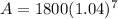
Solve.
A = 2368.68 <= rounded to 2 decimal places
The ending balance in her account is $2368.68.