Question

Can someone please help me with this problem? I don’t know how to do it. Thank you! :)

Answer 1

line K: y = -1.25 X + 3.5

function line J: y = 0.8 X + 6.625

Explanation:

slope of line m: Sm = (2-(-1)) / (5 - (-3)) = 3/8

line n // line m: slope N = Slope M

function line n : f(x) = 3/8 X + b

∴ 5 = 3/8 x 4 + b (y intercept of line N)

b = 5 - 3/2 = 7/2

fuction of line K: y=mx + b y= (6 - 3.5) / (-2 - 0) X + 3.5

line K: y = -2.5/2 * X + 3.5 = (-5/4) * X + 3.5

line J perpendicular to line K, so slope of line J equals to negative reciprocal of line K : 4/5

fuction of line J: y = 4/5 * X + B

6 = 4/5 * (-2) + b

b= 6- (- 8/5) =6+5/8

function line J: y = 4/5 * X + 6 5/8

Answer 2

a. The equation of line k in slope-intercept form is y = -8/3(x) + 2/3.

b. The equation of line j in slope-intercept form is y = 3/8(x) + 27/4.

In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):

`y - y_1 = m(x - x_1)`

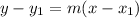
Where:

• x and y represent the data points.
• m represent the slope.

Since transversal k cuts through lines n and m with two same-side interior angles that are supplementary formed, we can logically deduce that both lines are parallel;

71° + 109° = 180°

Also, line k is perpendicular to lines j, m, and n because transversal k bisects line j at a right angle (90 degrees).

Next, we would determine the slope of line m;

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

Slope (m) = (2 + 1)/(5 + 3)

Slope (m) = 3/8

Part a.

Since line k is perpendicular to lines n and m, their slopes must be negative reciprocal of each other;

-8/3 × 3/8 = -1

At data point (-2, 6) and a slope of -8/3, an equation for line k can be calculated by using the point-slope form as follows:

y - 6 = -8/3(x + 2)

y = -8/3(x) - 16/3 + 6

y = -8/3(x) + 2/3

Part b.

Since line j is parallel to lines n and m, their slopes must be the same;

3/8 = 3/8

At data point (-2, 6) and a slope of 3/8, an equation for line k can be calculated by using the point-slope form as follows:

y - 6 = 3/8(x + 2)

y = 3/8(x) + 3/4 + 6

y = 3/8(x) + 27/4