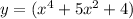Answer:
So the answer is
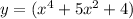
Explanation:
Given;
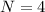 , 'I' and '2I' are zeros and
, 'I' and '2I' are zeros and
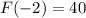 (equation-1)
(equation-1)
Assuming you need real coefficients so you use complex conjugate roots;
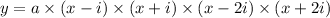 Where
Where
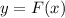
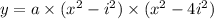 (By applying
(By applying
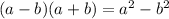 )
)
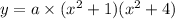 (We know
(We know
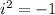 )
)
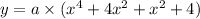
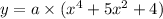 (equation-2)
(equation-2)
From equation;
 and
and
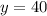
Plug 'x' and 'y' value in equation-2,
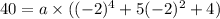
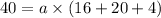
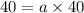
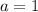
Now equation-2 become;
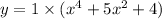
∴