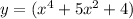Question

N=4
I and 2 I are zeros
F(-2)=40

Answer 1

So the answer is
`y= (x^(4) +5x^(2)+4 )`

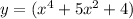
Explanation:

Given;

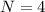`N=4` , 'I' and '2I' are zeros and

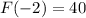`F(-2)=40` (equation-1)

Assuming you need real coefficients so you use complex conjugate roots;

`y=a*(x-i)* (x+i)* (x-2i)* (x+2i)` Where
`y=F(x)`

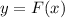
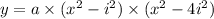`y=a* (x^(2) -i^(2) )* (x^(2) -4i^(2) )` (By applying
`(a-b)(a+b)=a^(2) -b^(2)`)

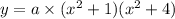`y=a*(x^(2)+1 )(x^(2)+4 )` (We know
`i^(2) =-1` )

`y=a* (x^(4)+4x^(2) +x^(2) +4 )`

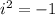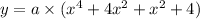
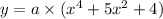`y=a* (x^(4)+5x^(2) +4 )` (equation-2)

From equation;

`x=-2` and
`y=40`

Plug 'x' and 'y' value in equation-2,

`40=a* ((-2)^(4)+5(-2)^(2) +4 )`

`40=a* (16+20+4)`

`40=a* 40`

`a=1`

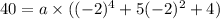
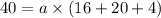
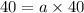
Now equation-2 become;

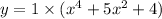
`y=1* (x^(4) +5x^(2)+4 )`

∴
`y= (x^(4) +5x^(2)+4 )`