Answer:
Ts = 413.66 K
Step-by-step explanation:
given data
temperature = 20°C
velocity = 10 m/s
diameter = 5 mm
surface emissivity = 0.95
surrounding temperature = 20°C
heat flux dissipated = 17000 W/m²
to find out
surface temperature
solution
we know that here properties of air at 70°C
k = 0.02881 W/m.K
v = 1.995 ×
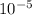 m²/s
m²/s
Pr = 0.7177
we find here reynolds no for air flow that is
Re =

Re =
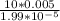
Re = 2506
now we use churchill and bernstein relation for nusselt no
Nu =
 = 0.3 +
= 0.3 +
![\frac{0.62 Re6{0.5}Pr^(0.33)}{[1+(0.4/Pr)^(2/3)]^(1/4)} [1+ ((2506)/(282000))^(5/8)]^(4/5)](https://img.qammunity.org/2020/formulas/engineering/college/qyazfkkymgdsr8jw2hcez363uw9dbk36fx.png)
h =
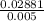 0.3 +
0.3 +
![\frac{0.62*2506{0.5}0.7177^(0.33)}{[1+(0.4/0.7177)^(2/3)]^(1/4)} [1+ ((2506)/(282000))^(5/8)]^(4/5)](https://img.qammunity.org/2020/formulas/engineering/college/saf7nj0yzjpkihsqbgh2eifj0iwtaisiuv.png)
h = 148.3 W/m².K
so
q conv = h∈(Ts- T∞ )
17000 = 148.3 ( 0.95) ( Ts - (20 + 273 ))
Ts = 413.66 K