Question

Consider a Carnot heat-engine cycle executed in a closed system using 0.028 kg of steam as the working fluid. It is known that the maximum absolute temperature in the cycle is twice the minimum absolute temperature, and the net work output of the cycle is 60 kJ. If the steam changes from saturated vapor to saturated liquid during heat rejection, determine the temperature of the steam during the heat rejection process.

Answer 1

T=138 °C

Step-by-step explanation:

Given that

m = 0.028 kg

Net work output W= 60 KJ

T₂=2T₁

As we know that efficiency of Carnot heat engine given as

`\eta=1-(T_1)/(T_2)`

`\eta=1-(T_1)/(2T_1)`

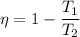
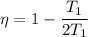
η = 0.5

We know that

`\eta=(W)/(Q_a)`

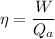
Qa=heat addition

W= net work output

`\eta=(W)/(Q_a)`

`0.5=(60)/(Q_a)`

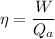
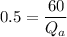
Qa= 120 KJ

From first law

Qa= W+ Qr

Qr= 120 - 60

Qr= 60 KJ

Qr Is the heat rejection.

Heat rejection per unit mass

Qr=60 / 0.028 = 2142.85 KJ/kg

Qr= 2142.85 KJ/kg

Temperature at which latent heat of steam is 2142.85 KJ/kg will be our answer.

T=138 °C

The temperature corresponding to 2142.85 KJ/kg will be 138 °C.

T=138 °C