Answer:
I = 80 A
Step-by-step explanation:
It is given that,
Mass of the wire, m = 14 g = 0.014 kg
Length of the wire, l = 16 cm = 0.16 m
Distance from wire,
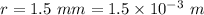
The force of gravity acting on the wire is balanced by the magnetic force. Mathematically, it is given by :
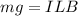
The magnetic field at the axis of wire is given by :
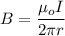
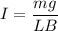
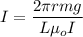
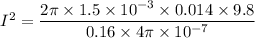
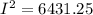
I = 80 A
So, the current flowing in the wire is 80 A. Hence, this is the required solution.