Since we have a fourth root, we want to find fourth powers inside it, so we can simplify them. There are three factors inside the root: a numeric one, one involving x and one involving y.
The number is 32, which is 2^5. This means that we can write it in this convenient way, which highlights the fourth power:
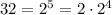
The factor involving x is very similar:
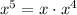
Finally, the factor involving y has only a third root, which is not enough.
So, we can rewrite our root as
![\sqrt[4]{32x^5y^3}=\sqrt[4]{2\cdot 2^4\cdot x\cdot x^4 y^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/b1xjv1tl1uvazx6nci99rkqvo3cdaeiiku.png)
And rearrange the terms like so:
![\sqrt[4]{2\cdot 2^4\cdot x\cdot x^4 y^3}=\sqrt[4]{2^4\cdot x^4\cdot x\cdot 2y^3}=\sqrt[4]{2^4\cdot x^4}\cdot \sqrt[4]{2xy^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/shgythuj6ygnq8nfmmsxygdjlug31f712c.png)
Simplify the fourth root and the fourth powers:
![\sqrt[4]{2^4\cdot x^4}\cdot \sqrt[4]{2xy^3}=2x\sqrt[4]{2xy^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pgpspiejolsl3kpbri7s867myt04m91fx7.png)
So, the whole expression is
![x^3\sqrt[4]{32x^5y^3}=2x^4\sqrt[4]{2xy^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mn9bd0tq5xs0ze3h5pcwrkqu01byw51bb4.png)