Question

Simplify the expression

Answer 1

Since we have a fourth root, we want to find fourth powers inside it, so we can simplify them. There are three factors inside the root: a numeric one, one involving x and one involving y.

The number is 32, which is 2^5. This means that we can write it in this convenient way, which highlights the fourth power:

`32=2^5=2\cdot 2^4`

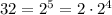
The factor involving x is very similar:

`x^5=x\cdot x^4`

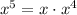
Finally, the factor involving y has only a third root, which is not enough.

So, we can rewrite our root as

`\sqrt[4]{32x^5y^3}=\sqrt[4]{2\cdot 2^4\cdot x\cdot x^4 y^3}`

And rearrange the terms like so:

`\sqrt[4]{2\cdot 2^4\cdot x\cdot x^4 y^3}=\sqrt[4]{2^4\cdot x^4\cdot x\cdot 2y^3}=\sqrt[4]{2^4\cdot x^4}\cdot \sqrt[4]{2xy^3}`

Simplify the fourth root and the fourth powers:

`\sqrt[4]{2^4\cdot x^4}\cdot \sqrt[4]{2xy^3}=2x\sqrt[4]{2xy^3}`

So, the whole expression is

`x^3\sqrt[4]{32x^5y^3}=2x^4\sqrt[4]{2xy^3}`