Question

A plane sound wave in air at 20°C, with wavelength 589 mm, is incident on a smooth surface of water at 25°C at an angle of incidence of 11.7°.

(a) Determine the angle of refraction for the sound wave.


(b) Determine the wavelength of the sound in water.

m

A narrow beam of sodium yellow light, with wavelength 589 nm in vacuum, is incident from air onto a smooth water surface at an angle of incidence of 11.7°.

(c) Determine the angle of refraction.



(d) Determine the wavelength of the light in water.

Answer 1

(a). The angle of refraction for the sound wave is 61.8°.

(b). The wavelength of the sound in water is 2.56 m.

(c). The angle of refraction is 8.26°.

(d). The wavelength of the light in water is 441.75 nm.

Step-by-step explanation:

Given that,

Wavelength = 589 mm

Incidence angle = 11.7°

We know that,

The speed of sound in water is GREATER than the speed of sound in air by a factor of about 4.3 times.

The speed of sound wave in water

`v_(w)= 1493\ m/s`

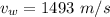
The speed of sound wave in air at 20°C

`v_(a)= 343\ m/s`

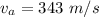
(a). We need to calculate the angle of refraction for the sound wave

Using Snell's law

`(\sin\theta_(1))/(v_(a))=(\sin\theta_(2))/(v_(w))`

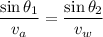
Put the value into the formula

`(\sin11.7)/(343)=(\sin\theta_(2))/(1493)`

`\sin\theta_(2)=(\sin11.7)/(343)*1493`

`\sin\theta_(2)=0.882`

`\theta_(2)=\sin^(-1)(0.882)`

`\theta_(2)=61.8^(\circ)`

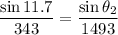
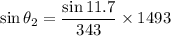
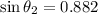
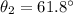
The angle of refraction for the sound wave is 61.8°.

(b). We need to calculate the wavelength of the sound in water

Using formula of wavelength

`(v_(w))/(\lambda_(w))=(v_(a))/(\lambda_(a))`

Put the value into the formula

`(1493)/(\lambda_(w))=(343)/(0.589)`

`\lambda_(w)=(1493*0.589)/(343)`

`\lambda_(w)=2.56\ m`

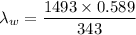
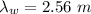
The wavelength of the sound in water is 2.56 m.

(c). We need to calculate the angle of refraction

Using formula of Snell's law

`n=(\sin\theta_(i))/(\sin\theta_(r))`

`(4)/(3)=(\sin11.7)/(\sin\theta_(r))`

`\sin\theta_(r)=(\sin11.7*3)/(4)`

`\theta_(r)=\sin^(-1)(0.1437)`

`\theta_(r)=8.26^(\circ)`

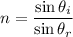
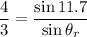
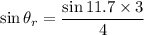
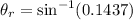
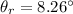
The angle of refraction is 8.26°.

(d). We need to calculate the wavelength of the light in water

Using formula of wavelength

`\lambda_(w)=(\lambda_(a))/(n)`

Put the value into the formula

`\lambda_(w)=(589)/((4)/(3))`

`\lambda_(w)=441.75\ nm`

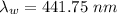
The wavelength of the light in water is 441.75 nm.

Hence, This is the required solution.