Answer:
(a). The angle of refraction for the sound wave is 61.8°.
(b). The wavelength of the sound in water is 2.56 m.
(c). The angle of refraction is 8.26°.
(d). The wavelength of the light in water is 441.75 nm.
Step-by-step explanation:
Given that,
Wavelength = 589 mm
Incidence angle = 11.7°
We know that,
The speed of sound in water is GREATER than the speed of sound in air by a factor of about 4.3 times.
The speed of sound wave in water
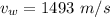
The speed of sound wave in air at 20°C
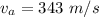
(a). We need to calculate the angle of refraction for the sound wave
Using Snell's law
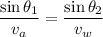
Put the value into the formula
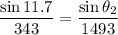
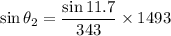
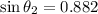
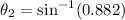
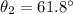
The angle of refraction for the sound wave is 61.8°.
(b). We need to calculate the wavelength of the sound in water
Using formula of wavelength
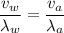
Put the value into the formula
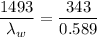
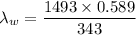
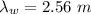
The wavelength of the sound in water is 2.56 m.
(c). We need to calculate the angle of refraction
Using formula of Snell's law
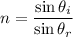
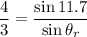
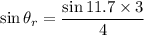
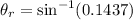
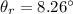
The angle of refraction is 8.26°.
(d). We need to calculate the wavelength of the light in water
Using formula of wavelength
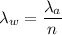
Put the value into the formula
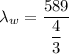
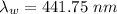
The wavelength of the light in water is 441.75 nm.
Hence, This is the required solution.