Question

Which graphs have rotational symmetry? Check all that apply

Answer 1

The answers are (A) & (C)

Explanation:

Your Welcome :D

Answer 2

Option A and C have rotational symmetry.

Explanation:

The graph of odd functions have rotational symmetry about its origin.

Here the first graph is a graph of f(x)=
`f(x)=x^3` which is an odd function bearing an exponent of 3.

A function is "odd" when we plug in any negative value in
`f(x)` then it gives negative of
`f(x)`.

And we also know that when a graph is mirroring about the y-axis then it is an even functions.

For even functions we have reflection symmetry rather than rotational symmetry.

The second graph is a graph of
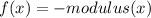`f(x)=-modulus (x)` which is an even function as we can see that its graph is mirroring about the y-axis.

The third graph is a graph of an ellipse which is possessing rotational symmetry.

The order of symmetry of an ellipse is generally 2.

Order of symmetry:

The order of rotational symmetry of an object is how many times that object is rotated and fits on to itself during a full rotation of 360 degrees.

So graph A and C have rotational symmetry.