Question

The temperature of a gas is related to its absolute pressure and specific volume through T = 3.488pv, where T, p, and v are expressed in their standard SI units. Consider a gas at 100 kPa and 1 m3/kg. (a) Estimate the change in temperature (ΔT) using Taylor's theorem if the state of the gas changes to 101 kPa and 1.01 m3/kg. (b) Compare your estimate with the exact change in temperature.

Answer 1

`0.425kPA \approx 0.43kPa`

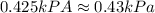
Step-by-step explanation:

In order to solve the problem we must resort to Taylor's approximations in which it is possible to obtain an approximation through a polynomial function.

For the particular case we proceed to make a linear approach.

Our values are defined as,

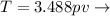`T = 3.488pv \rightarrow`Relation of temperature, pressure and volume

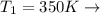`T_1 = 350K \rightarrow` Initial Temperature

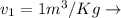`v_1 = 1m^3/Kg \rightarrow` Specific Volume

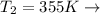`T_2 = 355K \rightarrow` Final Temperature

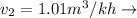`v_2 = 1.01m^3/kh \rightarrow` Final Specific Volume

The previous equation can be expressed as function of pressure, i.e,

`P = (T)/(3.488v)`

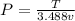
We can differentiate the expression in function of temperature and the specific volume, then

Temperature:

`(dP)/(dT) = (1)/(3.488v)`

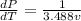
Volume

`(dP)/(dv) = -(T)/(3.488v^2)`

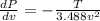
PART A) Then the total change of the pressure is given by,

`\Delta P = (dP)/(dT) + (dP)/(dv)`

`\Delta P =  (1)/(3.488v)(T_2-T_1)-(T)/(3.488v^2)(v_2-v_1)`

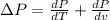
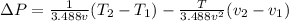
Replacing the values given, we have

`\Delta P =  (1)/(3.488(1.01))(355-350)-(355)/(3.488(1.01)^2)(1.01-1)`

`\Delta P = 0.43kPa`

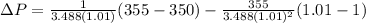
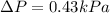
PART B) Now we can calculate the exact change in pressure through the general equation, that is

`\Delta P = (1)/(3.488)((T_2)/(v_2)-(T_1)/(v_1))`

Replacing the values we have:

`\Delta P =  (1)/(3.488)((355)/(1.01)-(350)/(1))`

`\Delta P = 0.425kPA`

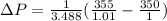
We can conclude that the approximation by Taylor's theorem is close to the value calculated by the general expression.