Answer: Our required probability is 0.1695.
Explanation:
Since we have given that
Number of male applicants = 4200
Number of female applicants = 3800
So, total number of applicants = 4200+3800 = 8000
Probability of male entered and subsequently enrolled is given by

Probability of female entered and subsequently enrolled is given by
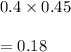
Number of male entered and subsequently enrolled is given by
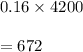
Number of female entered and subsequently enrolled is given by
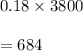
So, Probability that a student who applied for admission will be accepted by the university and subsequently will enroll is given by
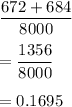
Hence, our required probability is 0.1695.