Question

The admissions office of a private university released the following admission data for the preceding academic year: From a pool of 4,200 male applicants, 60% were accepted by the university, and of these, 40% subsequently enrolled. Additionally, from a pool of 3,800 female applicants, 40% were accepted by the university, and of these, 45% subsequently enrolled. What is the probability that a student who applies for admission will be accepted by the university and subsequently will enroll?

Answer 1

Answer: Our required probability is 0.1695.

Explanation:

Since we have given that

Number of male applicants = 4200

Number of female applicants = 3800

So, total number of applicants = 4200+3800 = 8000

Probability of male entered and subsequently enrolled is given by

`0.4* 0.4=0.16`

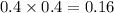
Probability of female entered and subsequently enrolled is given by

`0.4* 0.45\\\\=0.18`

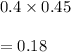
Number of male entered and subsequently enrolled is given by

`0.16* 4200\\\\=672`

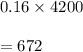
Number of female entered and subsequently enrolled is given by

`0.18* 3800\\\\=684`

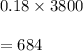
So, Probability that a student who applied for admission will be accepted by the university and subsequently will enroll is given by

`(672+684)/(8000)\\\\=(1356)/(8000)\\\\=0.1695`

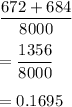
Hence, our required probability is 0.1695.