Answer:
D.A'(4,16),B'(4,13),C'(8,16)
Explanation:
We are given that triangle ABC has vertices at A(4,2),B(1,2) and C(4,6) in the coordinate plane.
First we change the given points

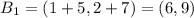
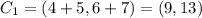
The rule of transformation of 270 degree rotation counterclockwise about origin is given by

After rotation 270 degrees about origin
Then,

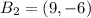
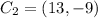
Apply the rule
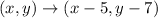
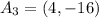
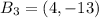
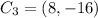
Hence, the coordinates of triangle ABC after 270 degrees counterclockwise rotation around (-5,-7) is given by
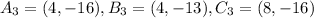
After rotation y=0
The rule of transformation about y=0 is given by
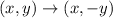
Apply this rule then we get
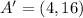
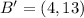

Hence, option D is true.