Answer:
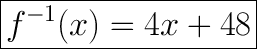
Explanation:
In order to find the inverse of a function, we need to follow a couple of steps.
- Step 1: Write the function as

- Step 2: Swap all x and y values
- Step 3: Solve for y
- Step 4: Replace y with
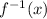
We can follow these steps to find the inverse of this function.
Step 1: We can just replace the f(x) with y, making our function
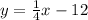 .
.
Step 2: We can swap where the x and y values are, making our equation

Step 3: We can now solve for y.
We now have the function as
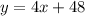 .
.
Step 4: We can now replace the y with
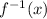 .
.

Therefore the inverse of
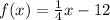 is
is
 .
.
Hope this helped!