Step-by-step explanation:
In an isotropic process, the equation is as follows.
![(T_(2))/(T_(1)) = [(P_(2))/(P_(1))]^{(k - 1)/(k)}](https://img.qammunity.org/2020/formulas/chemistry/college/ady4b05zw8e3nb2irw54rn4z83twvts6de.png)
![T_(2) = T_(1) * [(P_(2))/(P_(1))]^{(k - 1)/(k)}](https://img.qammunity.org/2020/formulas/chemistry/college/eoza9lzkr11ldh336wc5lnyl25zwwtzgs7.png)
As the given data is as follows.
 = 500 K, m = 5 kg
= 500 K, m = 5 kg
 = 5 bar,
= 5 bar,
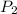 = 1 bar
= 1 bar
Now, putting the given values into the above formula as follows.
![T_(2) = T_(1) * [(P_(2))/(P_(1))]^{(k - 1)/(k)}](https://img.qammunity.org/2020/formulas/chemistry/college/eoza9lzkr11ldh336wc5lnyl25zwwtzgs7.png)
![T_(2) = 500 K * [(5 bar)/(1 bar)]^{(1.4 - 1)/(1.4)}](https://img.qammunity.org/2020/formulas/chemistry/college/2hh5qwhx6znvqz080om4215zd4as62yob8.png)
= 315.7 K
As according to the ideal gas equation, PV = mRT
So, calculate the volume as follows.
V =

=
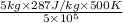 (as 1 bar = 10^{5} Pa[/tex])
(as 1 bar = 10^{5} Pa[/tex])
=
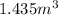
Now, we will calculate the value of
 as follows.
as follows.
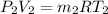
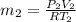
=
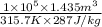
= 1.58 kg
Thus, we can conclude that the amount of mass remaining in the tank is 1.58 kg and its temperature is 315.7 K.