Question

Identify any zeros of


`y = {x}^(2) + 4x + 5`

a: (0,0)
b: there are no zeros
c: (-1,0), (-3,0)
d: (5,0), (4,0)​

Answer 1

b: There are no zeros

Explanation:

y = x² + 4x + 5

The parabola opens upward, because the coefficient of x² is positive.

Thus, the vertex is a minimum.

a = 1; b = 4; c = 5

The vertex form of a parabola is

y = (x - h)² + k

where (h, k) is the vertex and

h = -b/(2a) and k = f(h)

`h = -(4)/(2*1) = -(4)/(2) = -2`

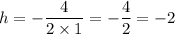
k = f(2) = (-2)² + 4(-2) + 5 = 4 - 8 + 5 = 1

The vertex is at (-2, 1).

The parabola never reaches the x-axis, so there are no zeros.

The graph below shows that your parabola has no real zeros.