Answer:
T=120.04°C
Step-by-step explanation:
Given that
L= 7.5 cm
q = 105 W/m³
T∞=120°C
h=750 W/m²K
K=20 W/mK
Here given that one side of the wall is insulated that is why the maximum temperature will be at the insulated surface.
The total heat transfer from the wall
Q= q A L
Q= 150 x 0.075 A
Q=7.875 A W
A=Area of wall
Now the total thermal resistance R
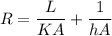

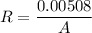
We also know that
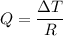
Temperature at insulated side = T
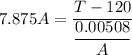

T=120.04°C