Question

A buoy starts at a height of 0 in relation to sea level and then goes up. Its maximum displacement in either direction is 6 feet, and the time it takes to go from its highest point to its lowest point is 4 seconds. Which of the following equations can be used to model h, the height in feet of the buoy in relation to sea level as a function of time, t, in seconds?

Answer 1

h= 6 sine (pi/4 times t)

Answer 2

`y=6sin((\pi)/(4)t)`

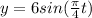
Explanation:

This problem is about an harmonic movement. The definition, that relates the given variables in this kind of movement is:

`y=Asin(\omega t)`

Where
`y` is the vertical displacement,
`t` is the time and
`\omega = (2 \pi)/(T)`

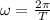
So, we just have find the angular frequency and then replace all given values:

`\omega = (2 \pi)/(T)=(2 \pi)/(8)=(\pi)/(4)`

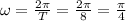
In this case, the period
`T` is 8 seconds, because according to the problem, half period is 4 second, from the highest point to the lowest, which is half of the complete period.

Now, replacing values:

`y=6sin((\pi)/(4)t)`

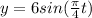
This expression, where
`y` is the height or vertical displacement, gives the height at any point.