Answer:
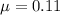
Step-by-step explanation:
It is given that,
Initial speed of the car, u = 25 m/s
Final speed of the car, v = 0 (it stops)
Distance travelled by the car when it slides, d = 275 m
Mass of the car, m = 755 kg
Let a is the acceleration of the car. Using the third equation of motion to find it as :
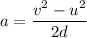
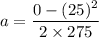
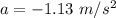
The car is decelerating.
Let
 is the coefficient of kinetic friction between the tires and the road. So,
is the coefficient of kinetic friction between the tires and the road. So,
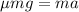
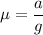
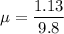
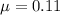
So, the coefficient of kinetic friction between the tires and the road is 0.11. Hence, this is the required solution.