Question

An old car is traveling down a long, straight, dry road at 25.0 m/s when the driver slams on the brakes, locking the wheels. The car comes to a complete stop after sliding 275 m in a straight line. If the car has a mass of 755 kg, what is the coefficient of kinetic friction between the tires and the road?

Answer 1

`\mu=0.11`

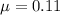
Step-by-step explanation:

It is given that,

Initial speed of the car, u = 25 m/s

Final speed of the car, v = 0 (it stops)

Distance travelled by the car when it slides, d = 275 m

Mass of the car, m = 755 kg

Let a is the acceleration of the car. Using the third equation of motion to find it as :

`a=(v^2-u^2)/(2d)`

`a=(0-(25)^2)/(2* 275)`

`a=-1.13\ m/s^2`

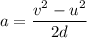
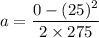
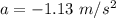
The car is decelerating.

Let
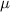`\mu` is the coefficient of kinetic friction between the tires and the road. So,

`\mu mg=ma`

`\mu=(a)/(g)`

`\mu=(1.13)/(9.8)`

`\mu=0.11`

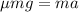
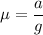
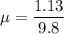
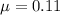
So, the coefficient of kinetic friction between the tires and the road is 0.11. Hence, this is the required solution.