Question

Jamal drew ΔLMN, in which m∠LMN = 90°. He then drew ΔPQR, which was a dilation of ΔLMN by a scale factor of 2 from the center of dilation at point M. Which of these can be used to prove ΔLMN ~ ΔPQR by the AA similarity postulate?

m∠P ≅ m∠N; this can be confirmed by translating point P to point N.

segment LM = 2segment PQ; this can be confirmed translating point P to point L.

m∠R ≅ m∠N; this can be confirmed by translating point R to point N.

segment MN = 2segment QR; this can be confirmed translating point R to point N.

Answer 1

C.
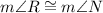`m\angle R\cong m\angle N`; this can be confirmed by translating point R to point N

Step-by step explanation:

We are given that

Triangle LMN in which
`\angle LMN=90^(\circ)`

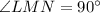
Triangle PQR is a dilation of triangle LMN by scale factor of 2 from the center of dilation at point M.

We have to find the statement that can be used to prove that triangle LMN is similar to triangle PQR by AA similarity postulates.

Dilation: It is that transformation in which shape of figure does not change but the size of figure changes.

Initial figure and final figure are similar in dilation .

Measure of angles or sides does not change only size changes in dilation transformation.

AA similarity postulate: When two angles of triangle are congruent to its corresponding angles of other triangle then, two triangle are similar by AA similarity postulate.

`\angle LMN=\angle PQR=90^(\circ)`

`m\angle R\cong m\angle N`

`\triangle LMN\sim \triangle PQR`

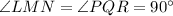
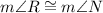
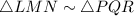
Reason: AA similarity postulate

Hence, option C is true.

Answer 2

C. m∠R ≅ m∠N; this can be confirmed by translating point R to point N

Explanation:

I took the test