Answer:
Option A is correct.
Explanation:
Given
To determine
What is the equation in the standard form of the line that passes through the point (4, −8) and has a slope of 1/4.
Using the point-slope form of the line equation
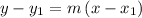
where
- m is the slope of the line
substituting the values m = 1/4 and the point (4, -8)
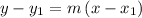
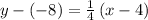
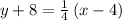
Subtract 8 from both sides

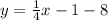
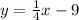
Writing the equation in the standard form
As we know that the equation in the standard form is
Ax+By=C
where x and y are variables and A, B and C are constants
so
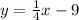

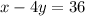
Therefore, the equation in the standard form of the line that passes through the point (4, −8) and has a slope of 1/4 will be:
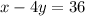
Hence, option A is correct.