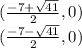For this case we have a function of the form:
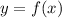
Where:
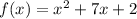
To find the intersections with the x-axis, we make
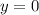 , that is:
, that is:

Where:

To find the solution we apply the following formula:
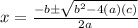
Substituting:

We have two roots:
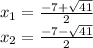
Thus, the intersections with the "x" axis are:
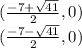
Answer: