Question

Lines s, t, and u are perpendicular bisectors of the sides of FGH and meet at J. If JG = 2x + 2, JH = 2y - 2, JF = 10 and HI = 2z - 4, find x, y, and z.

Question 16 options:



A) x = 4, y = 6, z = 7



B) x = 6, y = 4, z = 3



C) x = 6, y = 4, z = 7



D) x = 3, y = 7, z = 3

Answer 1

x = 4, y = 6, z = 7

Explanation:

Given that for a triangle FGH, lines s, t and u are perpendicular bisectors.

They concur at the point J.

We know that the point of concurrence of perpendicular bisectors is the circmcenttre of the triangle. Hence we will have J equidistant from the three vertices. In other words,

JG = JH=JF

`2x+2 = 2y-2 = 10\\x =4, y = 6`

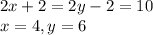
Now to find Z we make use of HI.

`JF =HI = 2z-4\\i.e. 10 = 2z-4\\z = 7`

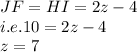
So option a is right answer

x = 4, y = 6, z = 7