Answer:
The spring stretches or compresses 0.8 m (80 cm)
Step-by-step explanation:
Hooke's Law
The force (F) needed to stretch or compress a spring by some distance Δx is given by
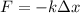
Where k is a constant factor characteristic of the spring.
We are given the constant of a spring k=50 N/m and it's required to calculate the displacement Δx produced by a force of F=40 N. Solving for Δx:
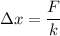
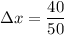
Calculating:
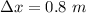
The spring stretches or compresses 0.8 m (80 cm)