Answer:
for random value of angle, one of initial velocities is > 21.6 m/s which is much above speed limit of 6.9 m/s(25 km/h)
Step-by-step explanation:
Force of friction causes deceleration,

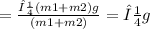
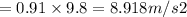
If v is velocity,
after collision, final velocity, vf = 0;
Applying,
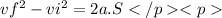
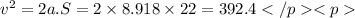
v = 19.81 m/s
Let first car moving along x axis and 2nd car moving along Y axis just before collision.
considering θ be angle of direction with x-axis of motion after collision.
Let v_1 and v2 be the velocities of 1st & 2nd cars before collision.
By using conservation of momentum along the x axis;

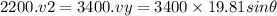
Hence, v1 = 56.13 cos θ
v2 = 30.62 sin θ
considering
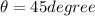
then v1 = 39.7 /s
v2 = 21.6 /s
The speed limit of 25 km/h = 6.9 m/s
For θ > 45 cos θ < 0.707; v1 < 39.7 m/s
But sin θ > 0.707; v2> 21.6 m/s
For θ < 45 cos θ > 0.707; v1 > 39.7 m/s
But sin θ < 0.707;v2 < 21.6 m/s
So, for random value of angle, one of initial velocities is > 21.6 m/s which is much above speed limit of 6.9 m/s(25 km/h).