Question

A smoking lounge is to accommodate 13 heavy smokers. The minimum fresh air requirement for smoking lounges is specified to be 30 L/s per person (ASHRAE, Standard 62, 1989). Determine the minimum required flow rate of fresh air that needs to be supplied to the lounge and the diameter of the duct if the air velocity is not to exceed 8 m/s

Answer 1

The minimum required flow rate of fresh air that needs to be supplied to the lounge is 390L/s.

The diameter of the duct mus be of 24.9cm at least if thte air velocity is not to exceed 8m/s.

Step-by-step explanation:

First, in order to find the minimum required flow rate of fresh air, we need to take the ASHRAE standard and multiply it by the number of heavy smokers, so we get:

`V'=30(L)/(s-persons)*13persons=390(L)/(s)`

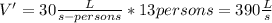
This value can be converted to
`m^(3)/s`

`390(L)/(s)*(1000cm^(3))/(1L)*(1m^(3))/((100cm)^(3))=0.39m^(3)/s`

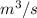
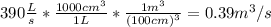
Once we got this value we use the volumetric flow formula, which tells us that:

`V'=Av`

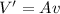
where A is the area of the duct and v is the velocity of the air flow.

We also know that:

`A=(\pi d^(2))/(4)`

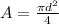
so we can substitute that into our equation, so we get:

`V'=(\pi d^(2))/(4)v`

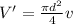
which can be solved for the diameter, which yields:

`d=\sqrt{(4V')/(\pi v)}`

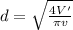
and we can next substitute the values the problem provides us with:

`d=\sqrt{(4()0.39m^(3)/s)/(\pi (8m/s))}=0.249m`

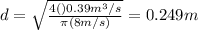
so the duct must have a diameter of at least 24.9cm for the velocity not to exceed 8m/s.