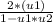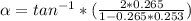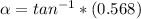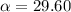Answer:
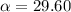
Step-by-step explanation:
Let the normal force of the wall on the ladder be N2 and the normal force of the ground on the ladder be N1.
Horizontal forces:
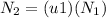 [1]
[1]
Vertical forces:
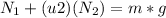 [2]
[2]
Substitute [2] into [1]:
![N_2 = (u1)*[m*g - (u2)(N_2)]](https://img.qammunity.org/2020/formulas/physics/high-school/exmnsavfq8s94ghb8k43fd7luob59zk1d6.png)
![N_2= ((u1)m*g)/([1 + (u1)(u2)])](https://img.qammunity.org/2020/formulas/physics/high-school/mr8b9u60mqwmi5hzh8358x4wov2d5u2gp2.png) [3]
[3]
Torques about the point where the ladder meets the ground:
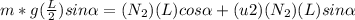
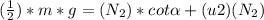
![[1 + (u1)(u2) - 2(u2)(u1)]/2 [1 + (u1)(u2)]= [(u1)/[1 + (u1)(u2)]]cot\alpha](https://img.qammunity.org/2020/formulas/physics/high-school/4rcy6580vy5cjud4ebl7lxsyq3sib85nxp.png)
tanα =