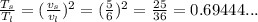Answer:
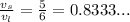
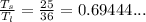
Step-by-step explanation:
The frequency of the nth harmonic on a string is given by the formula:
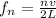
which can be written as:

Since the fundamental frequency means n=1, the ratio of the speed of waves on the shorter string (
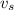 ) to the speed of waves on the longer string (
) to the speed of waves on the longer string (
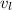 ) will be:
) will be:
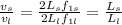
Since the frequencies are the same, and for our values is:

The speed of the waves relates to the tension and mass per unit length by the formula:
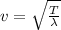
which can be written as:
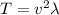
The ratio of the tension in the shorter string to the tension in the longer string will be:
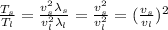
Since the mass per unit length are the same, and for our values is: