Question

A cantilever timber beam with a span of L = 4.25 m supports a linearly distributed load with maximum intensity of w0 = 5.5 kN/m. The allowable bending stress of the wood is 7.0 MPa and the allowable shear stress is 875 kPa. If the aspect ratio of the solid rectangular timber is specified as h/b = 0.67, determine the minimum width b that can be used for the beam.

Answer 1

the minimum width is b= 0.1414m = 141mm

Step-by-step explanation:

]given,

L= 4.25

w₀ = 5.5kN/m,

allowable bending stress = 7MPa

allowable shear stress = 875kPa

h/b = 0.67

b = ?

for a linearly distributed load, with maximum load intensity, w₀ of 5.5kN/m,

the maximum moment, M exerted by the timber is =

given h/b = 0.67, i.e h=0.67b

allowable bending stress =
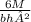`(6M)/(bh²)` = 7000kPa

7000 = (6*6.37)/ (b *(0.67b)² ) = 38.21/0.449b³

3080b³=38.21

b³ = 38.21/3080 = 0.0124

b = 0.232m

h=0.67b = 0.67* 0.232 = 0.155m

for allowable shear stress = (3V)/(2bh)

875 = (3V)/(2bh) = (3x 7.79)/(2xbx0.67b)

875 = 23.375/1.34b²

1172.5 b²= 23.375

b² =0.0199

b= 0.1414m

h=0.67b = 0.67* 0.1414 = 0.095m

the minimum width is b= 0.1414m = 141mm