Question

When Ryan is serving at a restaurant, there is a 0. 75 probability that each party will order drinks with their meal. During one hour, Ryan served 6 parties. Assuming bc that each party is equally likely to order drinks, what is the probability that at least one party will not order drinks?

Answer 1

0.82

Explanation:

Answer 2

0.82

Explanation:

We are given that

Total number of parties=n=6

The probability that each party will order drinks with their meal,q=0.75

The probability that party will not order drink with their meal=p=1-0.75=0.25

We have to find the probability that at least one party will not order drinks with their meal

Binomial probability distribution

`P(x=r)=nC_rq^(n-r)p^r`

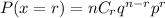
Using the formula

`P(x=0)=6C_0(0.75)^6`

`P(x=0)=(6!)/(6!)(0.75)^6`

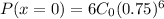
Using formula;
`nC_r=(n!)/(r!(n-r)!)`

`P(x=0)=(0.75)^6`

`P(x\geq 1)=1-P(x=0)`

`P(x\geq 1)=1-(0.75)^6`

`P(x\geq 1)=0.82`

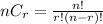
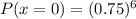
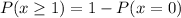
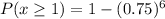
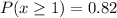
Hence, the probability that at least one party will not order drinks=0.82