Answer:
One Line
Explanation:
Important Information Given:
Let coordinate axes at the straight line be (a,0) and (0,b).
Thus, the equation of the straight line is,
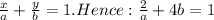
Equation: 4a + 2b =ab
Area of the triangle formed =
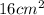
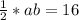
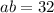
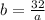
Substitute this value of b in the equation:

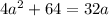
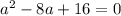
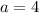
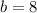
Hence, Only one straight line.
[RevyBreeze]