Question

Objects of equal mass are oscillating up and down in simple harmonic motion on two different vertical springs. The spring constant of spring 1 is 230 N/m. The motion of the object on spring 1 has twice the amplitude as the motion of the object on spring 2. The magnitude of the maximum velocity is the same in each case. Find the spring constant of spring 2.

Answer 1

`k_2=920\ N/m`

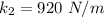
Step-by-step explanation:

Given that,

The spring constant of spring 1,
`k_1=230\ N/m`

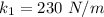
The motion of the object on spring 1 has twice the amplitude as the motion of the object on spring 2,
`A_1=2A_2`

As the magnitude of the maximum velocity is the same in each case, it means the maximum kinetic energy is same in each case. In other words, the total energy is same.

`(1)/(2)k_1A_1^2=(1)/(2)k_2A_2^2`

`k_1A_1^2=k_2A_2^2`

`k_1(2A_2)^2=k_2A_2^2`

`k_2=920\ N/m`

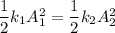
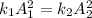
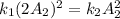
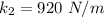
So, the spring constant of spring 2 is 920 N/m. Hence, this is the required solution.