Question

Three children are riding on the edge of a merry-go-round that is 105 kg, has a 1.40-m radius, and is spinning at 16.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm? Ignore friction, and assume that the merry-go-round can be treated as a solid disk and the children as points.

Answer 1

20.16744 rpm

Step-by-step explanation:

Initial angular momentum=Final angular momentum

Initial angular momentum=
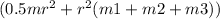`(0.5mr^(2)+ r^(2)(m1+m2+m3))` w1 hence
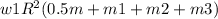`w1R^(2)(0.5m+m1+m2+m3)` where w1 is initial rate of rotation/ velocity, m is mass of merry go round, m1 is mass of first child, m2 is mass of second child, m3 is mass of the third child, r is the radius of merry go round

Final angular momentum=
`(0.5mr^(2)+ r^(2)(m1+m3))w2`

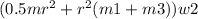
Substituting 105 Kg for m, 1.4 m for r, 16 rpm for w1, 22 Kg for m1, 28 Kg for m2, 33 Kg for m3 we obtain

1.4*16*((0.5*105)+{22+28+33})=1.4*w2((0.5*105)+{22+33})

`W2=\frac {1.4*16*((0.5*105)+{22+28+33})}{1.4*((0.5*105)+{22+33})}`

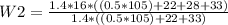
W2=20.16744 rpm