Answer:
The coefficient of friction is 0.38.
Step-by-step explanation:
The free body diagram is drawn below.
Let
 be frictional force acting in the backward direction as shown. Let the coefficient of friction be
be frictional force acting in the backward direction as shown. Let the coefficient of friction be
 . Let
. Let
 be the normal reaction force acting on the bag.
be the normal reaction force acting on the bag.
Given:
Mass of the bag is,

Force acting at
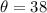 ° is
° is
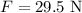
Acceleration due to gravity is,

The force F can be resolved into its components as
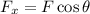 and
and
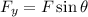
Therefore,
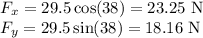
Now, as there is no acceleration in vertical direction, therefore,
Sum of upward forces = Sum of downward forces
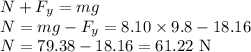
Now, as the bag is moving at a constant speed, so acceleration in the horizontal direction is also zero as acceleration is the rate of change of velocity.
Therefore, backward force = forward force.
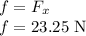
Now, frictional force is given as:
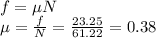
Therefore, the coefficient of friction is 0.38.