Answer:
A score of 4.2 on a test with a mean of 2.5 and a standard deviation of 1.2 has the highest relative position.
Explanation:
Which score has the highest relative position: a score of 38 on a test with a mean of 30 and a standard deviation of 10, a score of 4.2 on a test with a mean of 2.5 and a standard deviation of 1.2 or a score of 432 on a test with a mean of 396 and a standard deviation of 40.
In order to find the solution, we need to calculate the z score value for each test.
The z score formula:
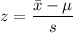 where
where
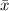 is the score, μ is the mean and s is the standard deviation.
is the score, μ is the mean and s is the standard deviation.
Now for test 1:
Put
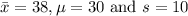 in the above formula.
in the above formula.
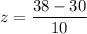
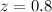
For test 2:
Put
 in the above formula.
in the above formula.
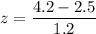
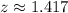
For test 3:
Put
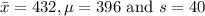 in the above formula.
in the above formula.
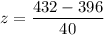
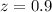
Since the z score value of test 2 is greater so a score of 4.2 on a test with a mean of 2.5 and a standard deviation of 1.2 has a highest relative position.