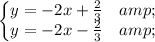Question

Which values of m and b will create a system of equations with no solution? Select two options. y = mx + b y = –2x + A system of equations. y equals m x plus b. y equals negative 2 x plus StartFraction 3 over 2 EndFraction. A coordinate grid with a line labeled y equals negative 2 x plus StartFraction 3 over 2 EndFraction and passes through the points (9, 1.5) and (1, 0.5). m = –3 and b = m equals negative 3 and b equals negative StartFraction 2 over 3 EndFraction. m = –2 and b = m equals negative 3 and b equals negative StartFraction 1 over 3 EndFraction. m = 2 and b = m equals 2 and b equals negative StartFraction 2 over 3 EndFraction. m = m equals StartFraction 3 over 2 EndFraction and b equals negative StartFraction 2 over 3 EndFraction and b = m equals negative StartFraction 3 over 2 EndFraction and b equals negative StartFraction 2 over 3 EndFraction m = -2 and b = m equals negative 2 and b equals negative StartFraction 2 over 3 EndFraction

Answer 1

m = -2 and b = -1/3

m = -2 and b = -2/3.

Explanation:

y = -2x - 1/3

y = -2x - 2/3

This system has no solutions because y cannot be 2 different values at once.

Answer 2

B, E

Explanation:

Given the first function:

`y=-2x+(2)/(3)`

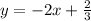
A Linear System with no solutions is graphically represented by two parallel lines, therefore with the same slope. So in this case, m has to be equal to -2.

And to this inconsistent system, if the linear parameter is not so relevant. So if m=-2 then b may be either equal to -1/3 or -2/3 according to the options.

Given the alternatives

No Solution System:

`\left\{\begin{matrix}y=-2x+(2)/(3) & \\ y=-2x-(1)/(3) & \end{matrix}\right.`

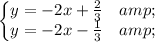
Or

`\left\{\begin{matrix}y=-2x+(2)/(3) & \\ y=-2x-(2)/(3) & \end{matrix}\right.`