Question

Your grandparents deposit $2,000 each year on your birthday, starting the day you are born, in an account that pays 7% interest compounded annually. How much will you have in the account on your 21st birthday, just after your grandparents make their deposit

Answer 1

The money you will have is $98020.

Step-by-step explanation:

It is given that grandparents deposit $2,000 each year on birthday and the account pays 7% interest compounded annually also the time is 21 years.

we will use the compound interest formula
`A=P (1 + (r)/(100))^(t)`.

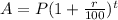For the first birthday the amount after 21 yr will be:

`A=2000(1+(7)/(100))^(21)`

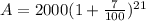
Similarly for the second birthday amount after 20yr will be:

`A=2000(1+(7)/(100))^(20)`

likewise, the last compound will be:

`A=2000(1+(7)/(100))^1`

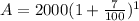
The total value of such compounding would be :

`\text {Total amount}=2000(1+(7)/(100))^(21)+2000(1+(7)/(100))^(20)...2000(1+(7)/(100))^(1)`

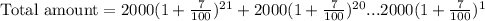
`\text {Total amount}=2000[(1+(7)/(100))^(21)+(1+(7)/(100))^(20)...(1+(7)/(100))^(1)]`

`\text{Total amount} \approx 2000(48.01)`

`\text{Total amount} \approx 96020`

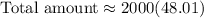
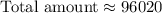
The total amount just after your grandparents make their​ deposit is:

≈($96020+2000)

≈$98020

Hence, the money you will have is $98020.