Question

Given the function, f(x)=sqrt 3x-3-3 , choose the correct transformation(s). Horizontal Compression, Right 1, Down 3 Horizontal Stretch, Right 3, Down 3 Vertical Compression, Right 1, Down 3 Vertical Stretch, Right 3, Down 3

Answer 1

Horizontal Compression, Right 1, Down 3.

Explanation:

|a| > 1 compression

horizontal bc inside square root

Answer 2

Horizontal Compression, Right 1, Down 3.

Explanation:

Given:

The transformed function is,
`f(x)=√(3x-3)-3`

Let the parent function be
`g(x) =√(x)`

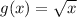
Now, in order to transform
`g(x)` to
`f(x)`, we need to perform the following transformations:

1.
`g(x)\rightarrow g(3x)=√(3x)`.

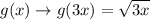Multiplying a positive number to the
`x` value of the function leads in horizontal compression.

2.
`g(3x)\rightarrow g(3(x-1))=√(3(x-1))=√(3x-3)`

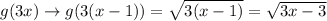
Adding a negative number to
`x` leads to a right shift of the function.

Here, the graph shifts right by 1 unit.

3.
`g(3(x-1))\rightarrow g(3(x-1)-3)=√(3x-3)-3`

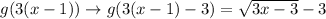
Adding a negative number to the function results in downward movement of the graph. Here, the graph moves down by 3 units.

Therefore, the order of correct transformations are:

Horizontal compression, Right shift by 1 units and then Down shift by 3 units.