Answer:
Horizontal Compression, Right 1, Down 3.
Explanation:
Given:
The transformed function is,
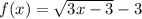
Let the parent function be
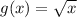
Now, in order to transform
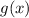 to
to
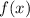 , we need to perform the following transformations:
, we need to perform the following transformations:
1.
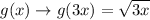 .
.
Multiplying a positive number to the
 value of the function leads in horizontal compression.
value of the function leads in horizontal compression.
2.
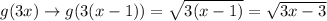
Adding a negative number to
 leads to a right shift of the function.
leads to a right shift of the function.
Here, the graph shifts right by 1 unit.
3.
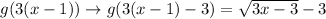
Adding a negative number to the function results in downward movement of the graph. Here, the graph moves down by 3 units.
Therefore, the order of correct transformations are:
Horizontal compression, Right shift by 1 units and then Down shift by 3 units.