Answer:
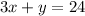
Step-by-step explanation:
Let the loaves sold be
 and rolls sold be
and rolls sold be
 .
.
Given:
Cost for 1 loaf of bread = $3
∴ Cost of
 loaves of bread =
loaves of bread =
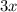
Cost of 1 roll of bread = $1
∴ Cost of
 rolls =
rolls =
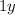
Total cost of the baked goods = $24
Therefore, as per question,
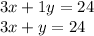
Now, the graph is shown below.
The vertical axis represent the rolls sold and the horizontal axis represent the loaves sold.
Draw a horizontal line from 12 mark on the vertical axis to the given line to meet at point A. Now, from point A, draw a vertical line to meet the horizontal axis at point B. Point B is the number of loaves sold.
From the graph, loaves sold are 4 when rolls sold are 12.