Answer:
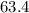 deg
deg
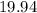 m
m
Step-by-step explanation:
 = mass of the heavier truck = 3 tonnes
= mass of the heavier truck = 3 tonnes
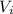 = velocity of truck before collision =
= velocity of truck before collision =
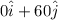 kmh⁻¹
kmh⁻¹
 = mass of lighter truck = 1 tonne
= mass of lighter truck = 1 tonne
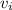 = velocity of lighter truck before collision =
= velocity of lighter truck before collision =
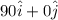 kmh⁻¹
kmh⁻¹
 = velocity of combination after collision
= velocity of combination after collision
Using conservation of momentum
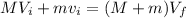
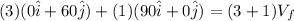
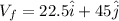
magnitude of the final speed is given as
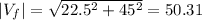 km/h
km/h
Direction is given as
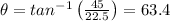 deg
deg
 = velocity of combination after collision = 50.31 km/h = 13.98 m/s
= velocity of combination after collision = 50.31 km/h = 13.98 m/s
 = velocity of combination after it comes to stop = 0 m/s
= velocity of combination after it comes to stop = 0 m/s
 = acceleration =
= acceleration =
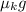 = -
= -
 = - 4.9 m/s²
= - 4.9 m/s²
 = stopping distance
= stopping distance
using the equation

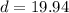 m
m